Understanding Quaternions: The Math Behind Smooth 3D Rotations

Quaternions are a powerful mathematical tool used extensively in computer graphics, robotics, and game development. Despite their complexity, quaternions offer an elegant solution for representing and manipulating rotations in 3D space. In this blog, we’ll explore what quaternions are, their mathematical foundation, and why they’re the go-to for 3D transformations in many fields.

1. Introduction to Quaternions

What Are Quaternions?

Quaternions are an extension of complex numbers, discovered by Sir William Rowan Hamilton in 1843. While complex numbers can represent rotations in 2D, quaternions handle rotations in 3D with ease. A quaternion qqq is generally written as:

q=a+b_i+c_j+d_k

Here, ais the real part, and b,c,d are the imaginary components. Unlike traditional 3D vectors, quaternions encapsulate both an axis of rotation and an angle, making them incredibly efficient for 3D rotations.

Why Use Quaternions?

Quaternions are popular in 3D applications because they don’t suffer from gimbal lock, a limitation of Euler angles that causes rotations to behave unpredictably. Quaternions are also computationally cheaper and more numerically stable than rotation matrices, making them ideal for animations, physics simulations, and virtual reality.

2. Mathematical Foundations

Structure of a Quaternion

A quaternion q=a+b_i+c_j+d_k consists of:

A scalar part a,
An imaginary vector part represented by (b,c,d).

Quaternions obey specific algebraic rules that allow for powerful manipulations in 3D space, but they also differ from ordinary numbers because quaternion multiplication is non-commutative (i.e., q₁⋅q₂≠q₂⋅q₁).

Basic Quaternion Operations

Addition and Subtraction work element-wise, just like vector addition.
Multiplication between two quaternions,q₁⋅q₂, combines their rotations and is more involved. This operation is key to chaining multiple rotations.
Norm: The norm 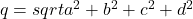$∣q∣= sqrt{a^2+b^2+c^2+d^2}$ measures a quaternion’s magnitude, which is essential for maintaining unit quaternions (quaternions of length 1) used in 3D rotations.

3. Geometric Interpretation

Quaternions as Rotations

In 3D space, quaternions can represent rotations around a specified axis. For a unit quaternion q representing a rotation, we can rotate a vector v by using the formula: $v'=qvq^{-1}$

Here, q^-1 is the inverse of q, which undoes the rotation represented by q. This formula is used extensively in 3D graphics and animation.

Visualizing Quaternion Rotations

Think of quaternions as rotating points on a sphere. They allow us to smoothly rotate from one orientation to another by taking the shortest path along this spherical surface. This makes them perfect for creating natural animations and avoiding gimbal lock issues.

4. Operations with Quaternions

Normalization

To ensure accurate rotations, we often normalize quaternions by dividing each component by the norm. This produces a unit quaternion, which represents a pure rotation without scaling.

Quaternion Conjugation and Inversion

The conjugate of a quaternion q=a+b_i+c_j+d_k is q^* = a – b_i – c_j – d_k, which is useful for reversing rotations. The inverse of a quaternion, given $q ^{-1} = \frac{q^*}{|q|^2}$ is used in rotation operations to undo a previous transformation.

Slerp (Spherical Linear Interpolation)

Slerp (Spherical Linear Interpolation) smoothly interpolates between two quaternions, often used to animate objects turning smoothly. This makes Slerp particularly valuable in game development, where objects need to rotate seamlessly between orientations.

5. Applications of Quaternions

Computer Graphics

In computer graphics, quaternions efficiently manage rotations of objects in 3D. They avoid the issues of gimbal lock and produce smooth, natural movements. Quaternions are particularly useful for camera rotations and the orientation of 3D models.

Game Development

Quaternions are essential in game development. Most game engines, like Unity and Unreal, use quaternions to control character movements, camera angles, and animation blending. They ensure smooth rotations without unpredictable snapping or flipping, which is critical for a seamless gaming experience.

public class Quaternion {
    double a, b, c, d; // Components of the quaternion
    public Quaternion(double a, double b, double c, double d) {
        this.a = a;
        this.b = b;
        this.c = c;
        this.d = d;
    }
    // Method to multiply two quaternions
    public Quaternion multiply(Quaternion q) {
        return new Quaternion(
            this.a * q.a - this.b * q.b - this.c * q.c - this.d * q.d,
            this.a * q.b + this.b * q.a + this.c * q.d - this.d * q.c,
            this.a * q.c - this.b * q.d + this.c * q.a + this.d * q.b,
            this.a * q.d + this.b * q.c - this.c * q.b + this.d * q.a
        );
    }
    // Method to normalize the quaternion
    public Quaternion normalize() {
        double norm = Math.sqrt(a * a + b * b + c * c + d * d);
        return new Quaternion(a / norm, b / norm, c / norm, d / norm);
    }
}

This Java code provides a basic structure for quaternion operations, and you can extend it to include other operations like conjugation, inversion, and Slerp.

7. Common Misconceptions and Challenges

Understanding 4D Nature

One challenge with quaternions is that they exist in 4D space, which can make visualizing them in 3D unintuitive. Think of them as encoding a rotation axis and an angle rather than trying to “see” them as a 4D entity.

Pitfalls in Quaternion Multiplication

Quaternion multiplication is non-commutative, so the order of multiplication matters. Switching the order of operations can produce entirely different rotations, which can lead to unexpected behaviors in animations.

Normalization Issues

Working with unnormalized quaternions can lead to scaling issues, as they won’t represent pure rotations. This is a common pitfall in implementing quaternion operations, so ensure that quaternions are normalized before applying them to rotations.

8. Conclusion

Quaternions are a fascinating and essential tool in 3D graphics, robotics, and game development. They provide smooth, gimbal-lock-free rotations and enable complex transformations with efficiency. Whether you’re a programmer, game developer, or math enthusiast, understanding quaternions opens doors to new possibilities in 3D applications.

To dive deeper, check out resources like Visualizing Quaternions by Andrew J. Hanson or explore libraries in your preferred programming language to get hands-on experience with these powerful entities.

Happy rotating!

Madhu Nanjipura